掲載情報は2015年8月現在
| 所属 | 大学院情報理工学研究科 情報・通信工学専攻 |

Yoshio OKAMOTO |
| メンバー | 岡本 吉央 教授 | |
| 所属学会 | European Association for Theoretical Computer Science、LAシンポジウム、Mathematical Optimization Society、電子情報通信学会、日本オペレーションズ・リサーチ学会 | |
| 研究室HP | http://dopal.cs.uec.ac.jp/okamotoy/ | |
| 印刷用PDF |
ネットワーク、離散アルゴリズム、離散幾何学、離散最適化、離散数学
米国の調査会社IDCの報告によると、2011年のデジタルデータの総量は1.8ZB(ゼタバイト:GBの1兆倍)に達し、ムーアの法則を上回る勢いで増え続けている。今、この大規模データをいかに活用するかが重要課題になっている。データを活用するためには、基本的なデータ処理を高速に行うことが必要となる。その処理を司るのが高速アルゴリズムだ。
当研究室では、離散数学(組合せ、順列、グラフなどの離散的な構造に関する数理の研究)の手法を使って問題を解析し、独自のアルゴリズムを使って最適なアウトプット(結果)を導き出す「離散最適化」を研究している。
データを整理すると、個々の特徴や数字が持つ相互関係が抽象的なネットワークや幾何学的な図形といった形で表せるものが多い。このようにデータを表現したものが数理モデルである。数理モデルを使うと整理されたデータをコンピュータで扱いやすくなる。この抽象的なネットワークをコンピュータで扱うための手法・方法論がグラフアルゴリズムで、その数学的基礎を与えているのがグラフ理論だ。一方、幾何学的な図形をコンピュータで扱うための手法・方法論が計算幾何学で、その数学的基礎を与えているのが離散幾何学だ。
離散最適化では離散的な数理モデルを処理して、その中から最適な部分を見つけ出す。最適化のターゲットは広く、相手の戦略を予想し自己の戦略を立てる際に用いる「ゲーム理論」も離散最適化の射程内にある。
この離散最適化を使って、障害物のある通路をロボットが効率良く通るためのルートを割り出したり、ワイヤレスネットワークにおいて干渉を考慮しながらサービスをより多く提供するためのアンテナの配置を決めたりといった、最適な解を世の中のあらゆるデータから抽出できる。
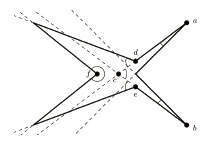
このように一連の作業をすべて行えるメリットは、解析して欲しいデータと、どのようなアウトプットが欲しいのかが決まれば、当研究室の手法や独自アルゴリズムを使って柔軟な解析ができることだ。例えば、より詳細なアウトプットが欲しい場合には数理モデル化の際の精度を上げてデータ抽出を行い、逆に簡易的なアウトプットで良ければ必要な部分のみを抽出する。これにより、アウトプット作成までの時間も調整が可能となり、津波の到達経路から最適な避難路を割り出す等の用途にも対応できる。この避難路の割り出しの場合なら、秒単位で変わるデータからすぐに結果を出力する必要があるので、データを瞬時に解析し、データの中から本当に必要な部分のみを抽出して数理モデル化し、アルゴリズムも軽くすることで、結果を即答できるものを作る。このように解析方法について適切にカスタマイズが行えるのは、一連の作業をすべてできる当研究室だからこそと言える。
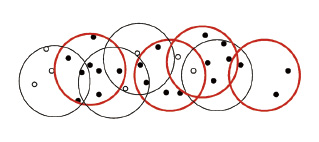
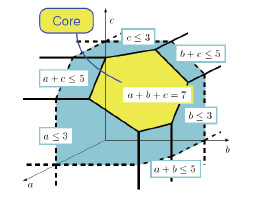
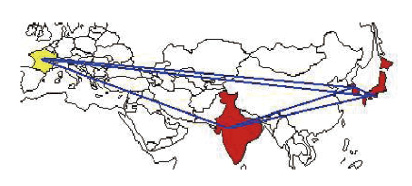
2012年、岡本は独創性と将来性に富む研究業績が認められ、オペレーションズ・リサーチ学会研究賞奨励賞を受賞した。
計算幾何学の応用範囲は広い。ロボット動作計画、ワイヤレスネットワーク、地理情報システムに現れるような見るからに幾何学的な問題の他にも、機械学習、データマイニングに現れる問題のように幾何学と関係なさそうなものの多くも、計算幾何学の問題として定式化できる。
基本的にはどのようなデータに対しても応用が効くため、常日頃さまざまなデータを解析して知見を広げている。特に、数理モデル化の作業は、より多くのデータを解析することで勘を鍛えることができるといわれている。現場の課題は良い経験となることから、今後は共同研究に積極的に取り組んでいきたい。
さらに、最終的には数学者として、勘という曖昧なものを計算機によって表現できるモデルにまで昇華していきたい。人間の考えていることはコンピュータでも捉えられるはずだ。そして、いつかはこの作業を数理モデル化し、誰でも最適化ができるような世界を夢見ている。